class: center, middle, inverse, title-slide # Causal survival analysis ## What If: Chapter 17 ### Elena Dudukina ### 2022-03-23 --- # 17.1 Hazards and risks - Average causal effect of smoking cessation on the time to death - The outcome is time to an event of interest that can occur at any time after the start of follow- up - Administrative end of follow-up - Competing events - If the competing event is not a censoring event, then the analysis sets the time to event to be infinite - If the competing event is a censoring event, then the analysis is an attempt to simulate a population in which death from other causes is abolished - Create a composite event that includes both the competing event and the event of interest (e.g., death and stroke) - Eliminates the competing events, but fundamentally changes the causal question - Restrict the inference to the principal stratum of individuals who would not die regardless of the treatment level they receive - Interpretation and valid estimation are hard - None of the above strategies provides a satisfactory solution to the problem of competing events --- # 17.1 Hazards and risks - Survival probability - `\(Pr[T > k]\)` - Risk - Cumulative incidence, at time k as one minus the survival: `\(1-Pr[T>k]=Pr[T<=K\)` - Hazard - The proportion of individuals at any time `\(k\)` who develop the event among those who had not developed it before `\(k\)` - `\(Pr [T = k|T > k − 1]\)` --- # Data .panelset[ .panel[.panel-name[Get data] ```r library(readxl) temp <- tempfile() temp2 <- tempfile() download.file("https://cdn1.sph.harvard.edu/wp-content/uploads/sites/1268/2017/01/nhefs_excel.zip", temp) unzip(zipfile = temp, exdir = temp2) data <- read_xls(file.path(temp2, "NHEFS.xls")) unlink(c(temp, temp2)) ``` ] .panel[.panel-name[Data] ```r library(tidyverse) library(magrittr) # define/recode variables data %<>% mutate( # censoring cens = if_else(is.na(wt82_71), 1, 0), # categorize the school variable (as in R code by Joy Shi and Sean McGrath) education = cut(school, breaks = c(0, 8, 11, 12, 15, 20), include.lowest = TRUE, labels = c('1. 8th Grage or Less', '2. HS Dropout', '3. HS', '4. College Dropout', '5. College or More')), active = factor(active), exercise = factor(exercise), survtime = if_else(death == 0, 120, (yrdth-83)*12 + modth) # yrdth ranges from 83 to 92 ) %>% filter(!is.na(education)) ``` ] ] --- # The hazards of hazard ratios .pull-left[ - The hazards vary over time; the hazard ratio generally does as well - "Single hazard ratio, which is usually the consequence of fitting a Cox proportional hazards model that assumes a constant hazard ratio by ignoring interactions with time" - Reported hazard ratio is a weighted average of the k-specific hazard ratios - Presenting the time-specific hazard ratios also do not have straightforward causal interpretation - 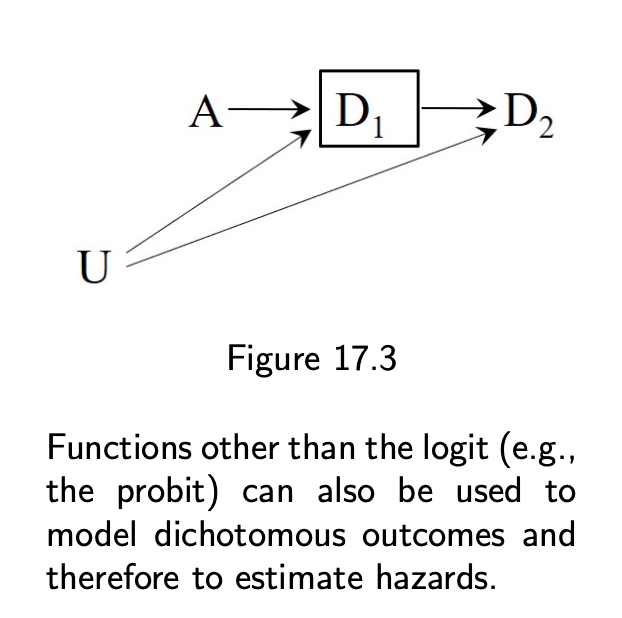Conditioning on the collider `\(D_1\)` will generally open the path A → `\(D_1\)` ← U → `\(D_2\)` and therefore induce an association between treatment A and event `\(D_2\)` among those with `\(D_1\)` = 0 ] .pull-right[  ] --- # Models for survival analysis - Accommodate the expected censoring of failure times due to administrative end of follow-up - Competing risk - Constructing nonparametric Kaplan-Meier curves means no assumptions about the distribution of the unobserved failure times due to administrative censoring - Parametric models for survival analysis assume a statistical distribution (e.g., exponential, Weibull) for the failure times or hazards - Semiparametric Cox proportional hazards model and the accelerated failure time (AFT) model, do not assume a particular distribution for the failure times or hazards - > Agnostic about the shape of the hazard when all covariates in the model have value of zero–often referred to as the baseline hazard - > Assume restrictions on the relation between the baseline hazard and the hazard under other combinations of covariate values --- # Approximating the hazard ratio via a logistic model - Discrete time HR - `\(\frac{Pr[D_{k+1}=1 |D_k=0, A=1]}{Pr[D_{k+1}=1|D_k=0, A=0]}\)` is `\(exp(\alpha_1\)`) at all times `\(k+1\)` in the hazards model `\(Pr[D_{k+1}=1|D_k=0, A] = Pr[D_{k+1}|D_k=0, A=0] exp(\alpha_1A)\)` - `\(log(Pr[D_{k+1}=1|D_k=0, A])=\alpha_{0,k} + \alpha_1k\)`, where `\(Pr[D_{k+1}=1|D_k=0, A=0]=\alpha_{0,k}\)` - When `\(k + 1\)` is small ➡️ `\(Pr[D_{k+1=1}|D_k=0, A=0]≈0\)`, the he hazard is ≈ to the odds - Odds: `\(\frac{Pr[D_{k+1}=1|D_k=0, A ]}{Pr[D_{k+1}=0|D_k=0, A]}\)` - `\(log(\frac{Pr[D_{k+1}=1|D_k=0, A ]}{Pr[D_{k+1}=0|D_k=0, A]})\)` = `\(logit(Pr[D_{k+1}=1|D_k=0, A])\)` = `\(\alpha_{0,k} + \alpha_1k\)` - If the hazard is close to zero at `\(k + 1\)`, one can approximate the log hazard ratio by a coefficient from a logistic model - Need to define a time unit `\(k\)` that is short enough for `\(Pr[D_{k + 1}=1|D_k = 0, A] < 0.1\)` to hold --- # 17.3 Why censoring matters - Not ready to assume that censoring is as if randomly assigned --- # 17.4 IP weighting of marginal structural models .pull-left[ - 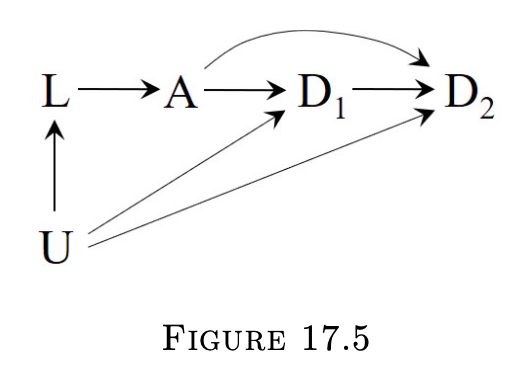In the situation of no exchageability between the treated and untreated, direct contrast of their survival curves is not warranted - L is sufficient for conditional exchangeability - Assume positivity and consistency ] .pull-right[  ] --- # 17.4 IP weighting of marginal structural models - Estimate the stabilized IP weight ```r ipw_num <- glm(qsmk ~ 1, data = data, family = binomial(link = "logit")) # denominator (propensity score model for the treatment) ipw_denom <- glm(qsmk ~ sex + race + age + I(age*age) + as.factor(education) + smokeintensity + I(smokeintensity*smokeintensity) + smokeyrs + I(smokeyrs*smokeyrs) + as.factor(exercise) + as.factor(active) + wt71 + I(wt71*wt71), data = data, family = binomial(link = "logit")) data %<>% mutate( # predicted probability of the treatment p_x = predict(ipw_num, type = "response"), p_x = case_when( qsmk == 1 ~ p_x, is.na(qsmk) ~ NA_real_, TRUE ~ 1 - p_x ), # predicted probability of the treatment given confounders p_x_l = predict(ipw_denom, type = "response"), p_x_l = case_when( qsmk == 1 ~ p_x_l, is.na(qsmk) ~ NA_real_, TRUE ~ 1-p_x_l ), # stabilized IPTW iptw_stab = p_x / p_x_l ) ``` --- # 17.4 IP weighting of marginal structural models - Using the person-time data format, fit a hazards model > 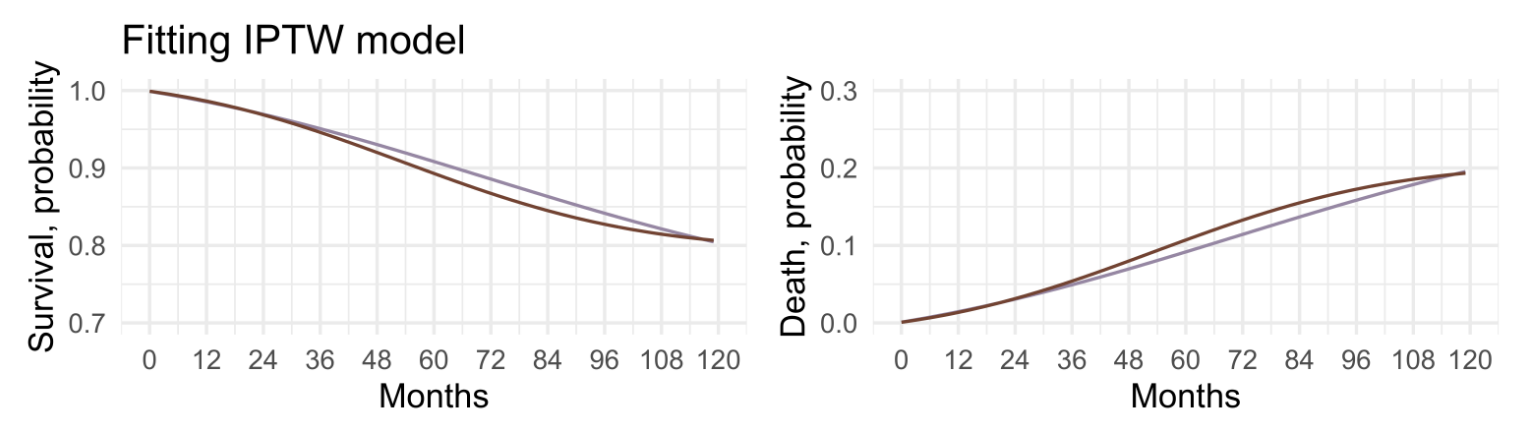The IP weighted model estimates the time-varying hazards that would have been observed if all individuals in the study population had been treated (a = 1) and the time-varying hazards if they had been untreated (a = 0)  - Plotting code is available [here](https://www.elenadudukina.com/post/hernan-chapter-17-viz-and-bootstrap/2021-01-18-what-if-chapter-17-viz-and-bootstrap/#section-173) --- # 17.4 IP weighting of marginal structural models > Though the survival curve under treatment was lower than the curve under no treatment for most of the follow-up, the maximum difference never exceeded −1.4% with a 95% confidence interval from −3.4% to 0.7%. > Little evidence of an effect of smoking cessation on mortality at any time during the follow-up. --- # 17.5 The parametric g-formula - Step 1: Fit a parametric hazards model ```r # expand original data set until the last observed month for everyone months_gform <- data %>% # using observed data and observed censoring times uncount(weights = survtime, .remove = F) %>% group_by(seqn) %>% mutate ( time = row_number() - 1, event = case_when( time == survtime -1 & death == 1 ~ 1, TRUE ~ 0 ), timesq = time*time ) %>% ungroup() %>% select(seqn, qsmk, time, timesq, age, sex, race, education, smokeintensity, smkintensity82_71, smokeyrs, exercise, active, wt71, event) # fitting Q-model (model for the outcome) with confounders and outcome predictors for better precision in observation-month data q_model <- glm(event == 0 ~ qsmk + I(qsmk*time) + I(qsmk*timesq) + time + timesq + sex + race + age + I(age*age) + as.factor(education) + smokeintensity + I(smokeintensity*smokeintensity) + smkintensity82_71 + smokeyrs + I(smokeyrs*smokeyrs) + as.factor(exercise) + as.factor(active) + wt71 + I(wt71*wt71), data = months_gform, family = binomial(link = "logit")) ``` --- # 17.5 The parametric g-formula - 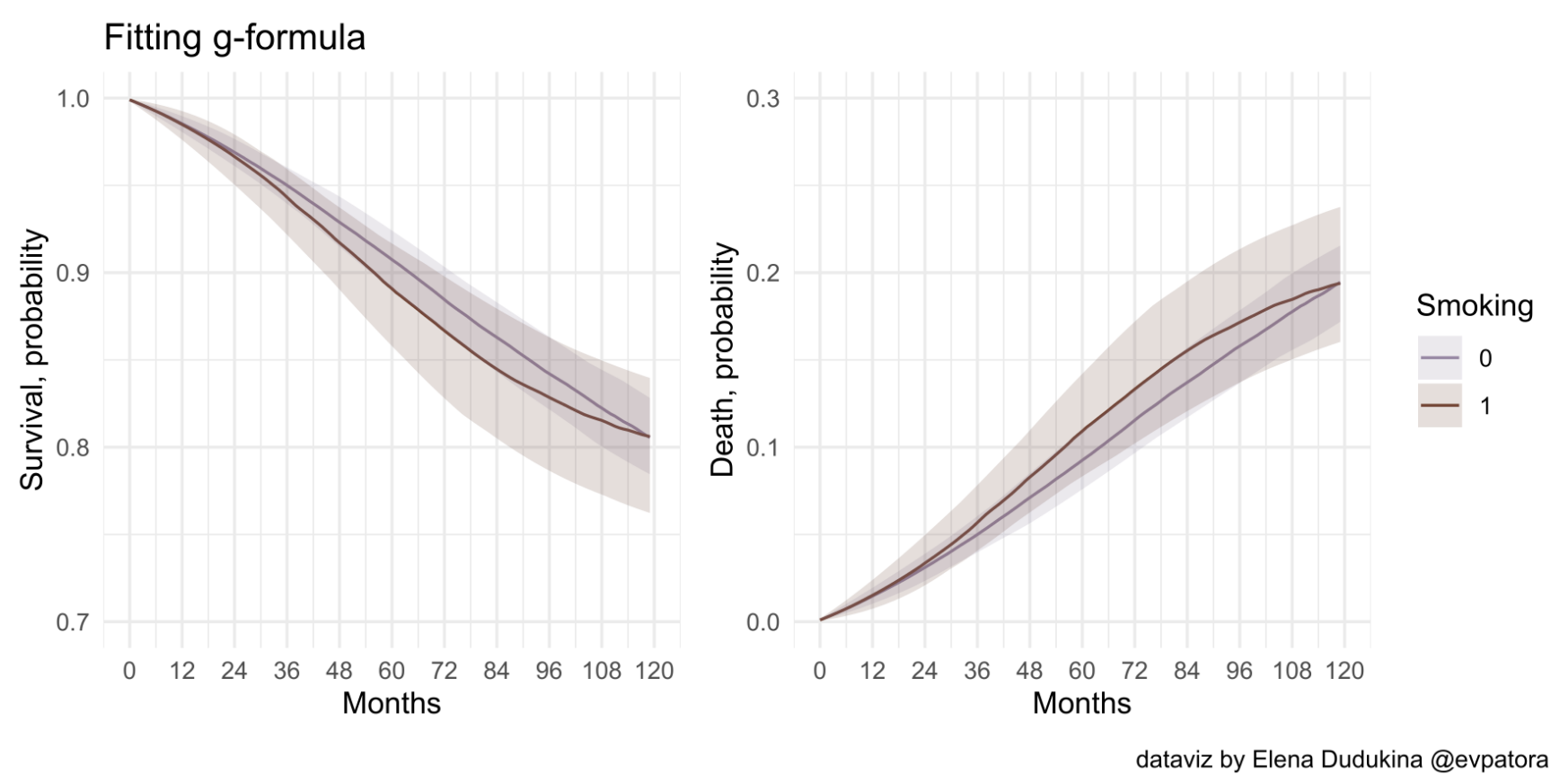Step 2: Compute the weighted average of the conditional survival across all values `\(l\)` of the covariates `\(L\)` (standardizing the survival to the confounder distribution)  - Plotting code is available [here](https://www.elenadudukina.com/post/hernan-chapter-17-viz-and-bootstrap/2021-01-31-what-if-chapter-17-viz-and-bootstrap-g-formula/#secton-174) --- # 17.5 The parametric g-formula > - After adjustment for the covariates L via standardization, we found little evidence of an effect of smoking cessation on mortality at any time during the follow-up. Note that the survival curves estimated via IP weighting and the parametric g-formula are similar but not identical because they rely on different parametric assumptions. > - The IP weighted estimates require no misspecification of a model for treatment and a model for the unconditional hazards. > - The parametric g-formula estimates require no misspecification of a model for the conditional hazards. --- # 17.6 G-estimation of structural nested models - Structural nested log-linear model to model the ratio of cumulative incidences (i.e., risks) under different treatment levels - Structural nested cumulative failure time model - Used when survival is rare because log-linear models do not naturally impose an upper limit of 1 on the survival - Accelerated failure time (AFT) model - Models the ratio of survival times under different treatment options - Rarely been used in practice due to the lack of user-friendly software - Parameters of structural AFT models estimated via search algorithms do not guarantee to find a unique solution --- # References 1. Hernán MA, Robins JM (2020). Causal Inference: What If. Boca Raton: Chapman & Hall/CRC (v. 30mar21) 1. [Causal Survival Analysis: IPTW and 95% CI bands](https://www.elenadudukina.com/post/hernan-chapter-17-viz-and-bootstrap/2021-01-18-what-if-chapter-17-viz-and-bootstrap/) 1. [Causal Survival Analysis: Parametric g-formula and and 95% CI bands](https://www.elenadudukina.com/post/hernan-chapter-17-viz-and-bootstrap/2021-01-31-what-if-chapter-17-viz-and-bootstrap-g-formula/)